播州区建设局网站市场调研报告范文
文章目录
- 优先级队列介绍
- 优先级队列使用
- 仿函数
- 优先级队列模拟实现
优先级队列介绍
优先队列是一种容器适配器 ,它的底层实现是堆,虽然它的名字里面有队列,但它并没有队列先进先出的特性

优先级队列定义在头文件中,其模板参数有三个,第一个是类型,第二个是结构,第三个则是指定底层实现是使用大堆还是小堆(默认是大堆)
关于第三个参数的实现就要提到一个语法知识–仿函数,下面会讲到。先来看看优先级队列的简单接口操作
优先级队列使用
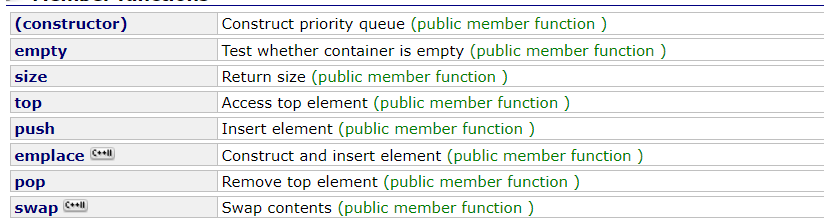
和之前的容器类似,优先级队列也有插入删除接口,这里要注意优先级队列并没有迭代器,因为如果优先级队列具有随机访问的话会破坏底层的堆结构
int main() {priority_queue<int> qe;qe.push(1);qe.push(3);qe.push(4);qe.push(8);for (int i = 0; i < 4; ++i) {cout << qe.top() << " ";qe.pop();}cout << endl;return 0;
}

可以看到如果我们定义一个优先级队列并且指定的模板参数只有第一个类型时,其默认的方式是大堆,因此当我们逐个取出数据时,无论插入数据的顺序如何都会在内部自动以大堆的形式排序好。
那么如果我们先要让其以小堆的形式存储呢。首先因为优先级队列的模板参数里面后面的两个参数都给定了缺省值,所以如果我们需要指定第三个参数时注意也要将第二个参数写上
指定大堆或小堆的头文件– 默认是大堆 greater是小堆 less是大堆
int main() {priority_queue<int, vector<int>, greater<int>> qe;qe.push(1);qe.push(3);qe.push(4);qe.push(8);for (int i = 0; i < 4; ++i) {cout << qe.top() << " ";qe.pop();}cout << endl;return 0;
}

以上就是优先级队列的简单使用,下面来一道OJ题练习一下,
数组中第k大元素
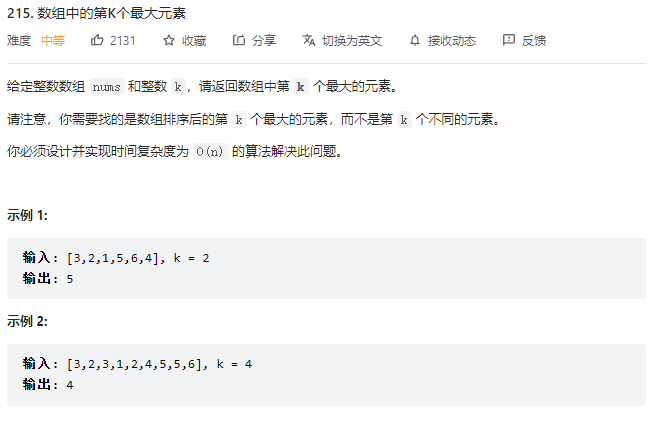
这道题要求找出一个数组中的第k大个元素,如果在之前没有了解过优先级队列,那我们就得对数组进行排序比较的麻烦,现在有了优先级队列我们就可以直接将数组中的每个元素插入到优先级队列中,然后将第k个元素前的元素pop掉之后取出顶部的元素即可
class Solution {
public:int findKthLargest(vector<int>& nums, int k) {//优先级队列区间构造priority_queue<int> qe(nums.begin(), nums.end());while (--k)qe.pop();return qe.top();}
};
仿函数
了解完优先级队列的简单使用,现在我们来看一下一个新的语法知识,仿函数。先来看一段代码
//仿函数
template<class T>
class myless {
public:bool operator()(const T& x, const T& y) {return x > y;}
};template<class T>
class mygreater {
public:bool operator()(const T& x, const T& y) {return x < y;}
};
上面的代码定义了两个类,类中重载了()运算符
myless<int> lessfunc;
cout << lessfunc(1, 2) << endl;
mygreater<int> greaterfunc;
cout << greaterfunc(1, 2) << endl;
乍一看上面的 lessfunc(1, 2),greaterfunc(1, 2) 可能会觉得像是在调用一个函数,实际上不是,这只是这两个类的实例化对象因为类重载了()操作符,所以用起来就跟函数一样,这样的类对象就可以称为仿函数。
优先级队列模拟实现
了解了仿函数,接下来就可以进行优先级队列的模拟实现了。
首先实现一个容器类,肯定得先定义好类的构造函数。因为优先级队列的底层是堆,所以我们肯定需要对元素进行建堆操作,那么建堆有两种方式–向上调整和向下调整,关于这两种方法可以参考之前关于堆的那篇文章。
因为我们需要做到根据模板参数不同而灵活做出大堆小堆的切换,所以建堆的方法中我们加入仿函数去进行比较这样才能实现对模式的切换
对于插入操作,每插入一个元素都得进行堆调整以保证堆结构不被破坏,因为元素插入是尾插,所以选用向上调整
对于删除操作,删除元素后也不能破坏堆结构,因为是删除数组顶部元素,所以选用向下调整法
template<class T>
class less {
public:bool operator()(const T& x, const T& y) {return x < y;}
};template<class T>
class greater {
public:bool operator()(const T& x, const T& y) {return x > y;}
};template<class T, class Container = vector<T>, class Compare = less<T>>
class priority_queue {
public:priority_queue(){}//区间构造函数template<class InputIterator>priority_queue(InputIterator first, InputIterator last):_con(first, last){//建堆for (int i = (_con.size() - 1 - 1) / 2; i >= 0; ++i)adjust_down(i);}//向上调整void adjust_up(size_t child) {//创建仿函数对象Compare com;size_t parent = (child - 1) / 2;while (child > 0) {//比较父与子元素,实现堆结构if (com(_con[parent], _con[child])) {swap(_con[child], _con[parent]);child = parent;parent = (child - 1) / 2;}elsebreak;}}//向下调整void adjust_down(size_t parent) {//创建仿函数对象Compare com;size_t child = parent * 2 + 1;while (child < _con.size()) {//找到较大的子元素if (child + 1 < _con.size() && com(_con[child], _con[child + 1]))child++;//比较父与子元素,实现堆结构if (com(_con[parent], _con[child])) {swap(_con[child], _con[parent]);parent = child;child = parent * 2 + 1;}elsebreak;}}void push(const T& x) {_con.push_back(x);adjust_up(_con.size() - 1);}void pop() {//交换首尾元素,删除原首元素swap(_con[0], _con[_con.size() - 1]);_con.pop_back();adjust_down(0);}const T& top() const{return _con[0];}bool empty() const {return _con.empty();}private://元素数组Container _con;
};