如何做解析网站seo技术培训学校
一,简单了解二分搜索树
树结构:
问题:为什么要创造这种数据结构
1,树结构本身是一种天然的组织结构,就好像我们的文件夹一样,一层一层的.

2,树结构可以更高效的处理问题
二,二分搜索树的基础
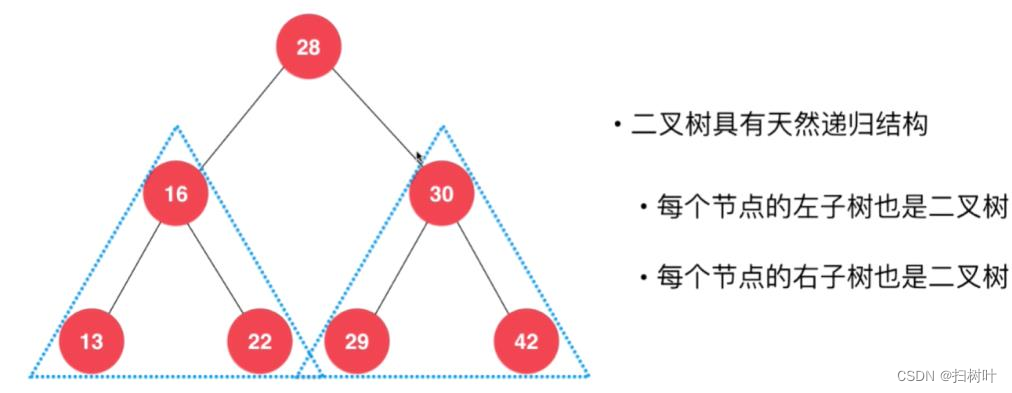
1、二叉树


2,二叉树的重要特性
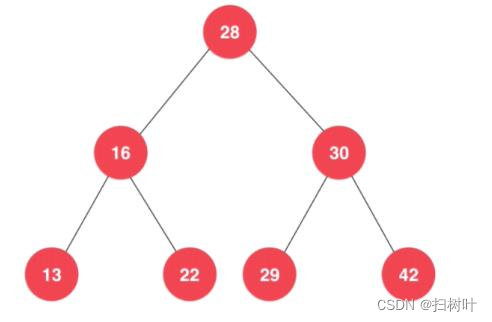
 满二叉树
满二叉树

总结:
1. 叶子结点出现在二叉树的最底层,除叶子结点之外的其它结点都有两个孩子结点。
2. 一个层数为k 的满二叉树总结点数为:
3. 第i层上的结点数为:
4. 一个层数为k的满二叉树的叶子结点个数(也就是最后一层):
4、二叉树不一定是“满”的
3,二分搜索树


(注意:存储的元素必须具有可比性)
1,向二分搜索树添加元素

2,向二分搜索树查询操作
1,递归终止的条件 : if(node == null ) return false;
2,递归操作
if (ele.compareTo(node.ele) < 0) {
return search(node.left, ele);
} else if (ele.compareTo(node.ele) > 0) {
return search(node.right, ele);
} else {
return true;
}
3,二分搜索树的遍历操作
遍历操作:把树中所有节点都访问一遍
1前序遍历,
2中序遍历,
3后序遍历
4层序遍历(广度优先)
(代码,会在后面一起展现.)
4,二分搜索树寻找最大值,最小值
 同样的原理找出二分搜素树中最大的元素,这里不在过多赘述.
同样的原理找出二分搜素树中最大的元素,这里不在过多赘述.
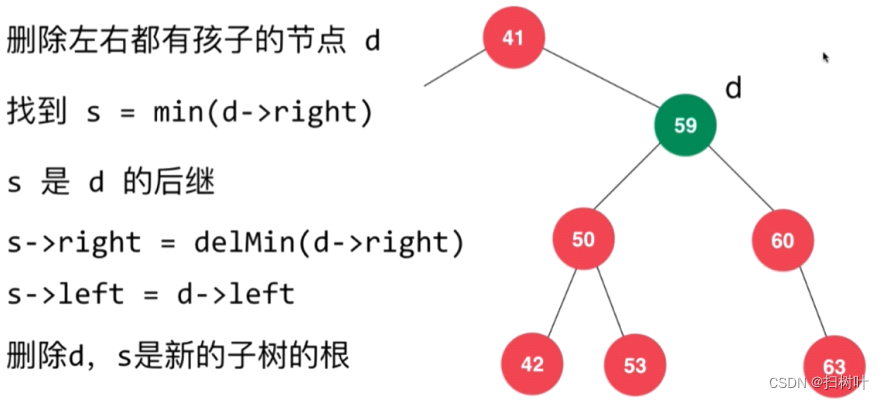
5,删除操作
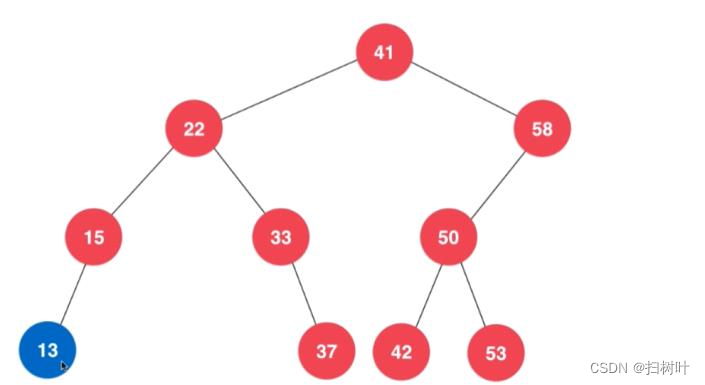
情况一:(叶子结点)
情况二、(非叶子结点)
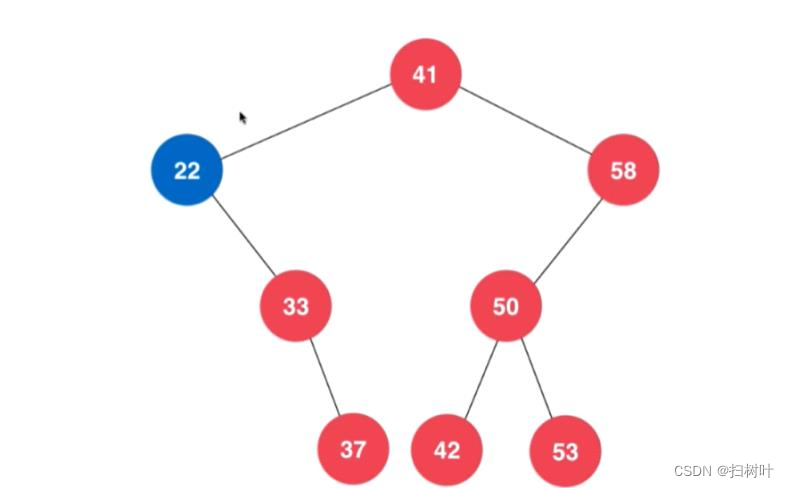
删除后
 6,删除二分搜索树中的节点
6,删除二分搜索树中的节点
情况一:
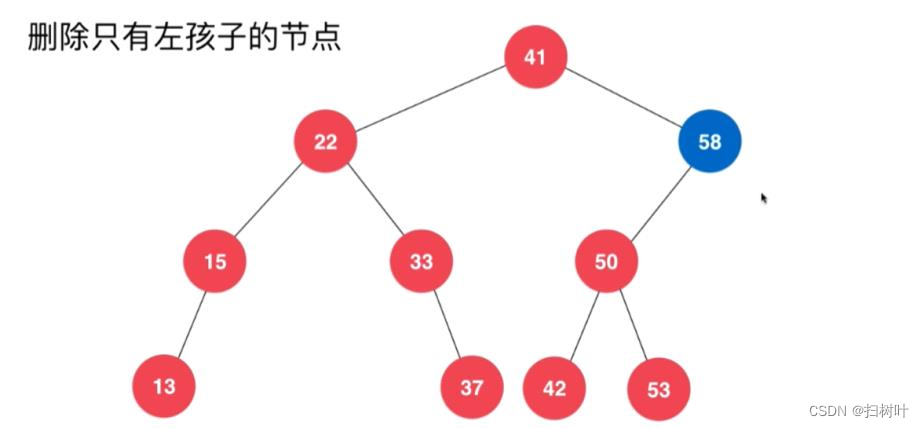
情况二、

情况三:左右孩子都不为空的情况
使用Hibbard Deletion

三,用代码实现二分搜索树.实现相关功能.
(由于功能实现较多,代码较长)
其中包含是前面的各种功能操作的实现,包括,前,中,后,层,序把遍历,删除,添加,等等操作.需要的同学可以仔细查看.
mport java.nio.channels.Pipe;
import java.util.*;
import java.util.stream.Collectors;// 二分搜索树
public class BinarySearchTree<T extends Comparable<T>> {// 定义树的结点public class Node {T val;Node left; // 左孩子Node right; // 右孩子public Node(T val) {this.val = val;}}// 定义树的根private Node root;// 树根// 统计树中结点的个数private int size;// 树中结点的个数public BinarySearchTree() {this.root = null;this.size = 0;}// 判断树是否为空public boolean isEmpty() {return this.size == 0;}// 获取树中元素的个数public int getSize() {return this.size;}// 向树中添加元素public void add(T val) {this.size++;this.root = add(this.root, val);}/*** 添加的递归方法** @param node 树的根结点* @param val 添加的值*/private Node add(Node node, T val) {//递归终止的条件if (node == null) {Node leafNode = new Node(val);return leafNode;}// 递归操作if (node.val.compareTo(val) > 0) {node.left = add(node.left, val);} else {node.right = add(node.right, val);}return node;}// 将树中所有结点进行遍历--中序遍历( 深度优先搜索 DFS,使用的栈来实现)public String middleTravel() {List<T> result = new ArrayList<>();middleTravel(this.root, result);return result.stream().map(item -> item.toString()).collect(Collectors.joining(","));}/*** 中序遍历** @param node 树的根结点*/private void middleTravel(Node node, List<T> result) {// 递归终止的条件if (node == null) {return;}// 递归操作// 先遍历左子树middleTravel(node.left, result);// 打印当前值result.add(node.val);// 再遍历右子树middleTravel(node.right, result);}public String beforeTravel() {List<T> result = new ArrayList<>();beforeTravel(this.root, result);return result.stream().map(item -> item.toString()).collect(Collectors.joining(","));}/*** 前序遍历** @param node 树的根结点*/private void beforeTravel(Node node, List<T> result) {// 递归终止的条件if (node == null) {return;}// 递归操作// 打印当前值result.add(node.val);// 先遍历左子树beforeTravel(node.left, result);// 再遍历右子树beforeTravel(node.right, result);}public String afterTravel() {List<T> result = new ArrayList<>();afterTravel(this.root, result);return result.stream().map(item -> item.toString()).collect(Collectors.joining(","));}/*** 后序遍历** @param node 树的根结点*/private void afterTravel(Node node, List<T> result) {// 递归终止的条件if (node == null) {return;}// 递归操作// 先遍历左子树afterTravel(node.left, result);// 再遍历右子树afterTravel(node.right, result);// 打印当前值result.add(node.val);}// 查找的方法public boolean contains(T val) {return contains(this.root, val);}/*** 从以node为根的二分搜索树中查找元素val** @param node 根节点* @param val 要搜索的值* @return*/private boolean contains(Node node, T val) {// 递归到底的情况if (node == null) {return false;}// 递归操作if (node.val.compareTo(val) == 0) {return true;} else if (node.val.compareTo(val) > 0) {return contains(node.left, val);} else {return contains(node.right, val);}}// 树的层序遍历(广度优先搜索 BFS,使用队列来实现)public String levelTravel() {List<String> list = new ArrayList<>();// 1、 创建一个队列Queue<AbstractMap.SimpleEntry<Integer, Node>> queue = new LinkedList<>();// 2、将根结点入入队if (this.root != null) {queue.offer(new AbstractMap.SimpleEntry<>(1, this.root));}// 3、遍历队列while (!queue.isEmpty()) {AbstractMap.SimpleEntry<Integer, Node> temp = queue.poll();Node value = temp.getValue();int key = temp.getKey();//3-1 先将内容保存list.add(value.val.toString() + "------" + key);// 3-2 判断左子树是否为空,不为空就入队if (value.left != null) {queue.offer(new AbstractMap.SimpleEntry<>(key + 1, value.left));}// 3-3 判断右子树是否为空,不为空就入队if (value.right != null) {queue.offer(new AbstractMap.SimpleEntry<>(key + 1, value.right));}}return list.stream().collect(Collectors.joining(","));}public List<List<T>> levelOrder() {// 返回值类型是啥,就创建啥List<List<T>> result = new ArrayList<>();// 1、 创建一个队列Queue<AbstractMap.SimpleEntry<Integer, Node>> queue = new LinkedList<>();// 2、将根结点入入队if (this.root != null) {queue.offer(new AbstractMap.SimpleEntry<>(1, this.root));}while (!queue.isEmpty()) {AbstractMap.SimpleEntry<Integer, Node> temp = queue.poll();Node value = temp.getValue();int key = temp.getKey();//3-1 先将内容保存if(result.get(key-1)==null){result.add(new ArrayList<>());}result.get(key-1).add(value.val);// 3-2 判断左子树是否为空,不为空就入队if (value.left != null) {queue.offer(new AbstractMap.SimpleEntry<>(key + 1, value.left));}// 3-3 判断右子树是否为空,不为空就入队if (value.right != null) {queue.offer(new AbstractMap.SimpleEntry<>(key + 1, value.right));}}return result;}// Pair对public class Pair<Node> {private Node value; // 保存值private int key; // 保存层public Pair(Node value, int key) {this.value = value;this.key = key;}public Node getValue() {return value;}public int getKey() {return key;}}// 从二分搜索树中找最小值(在整棵树的最左边)public T getMinVal() {// 判断树是否为空if (this.root == null) {return null;}Node curNode = this.root;while (curNode.left != null) {curNode = curNode.left;}return curNode.val;}public T getMinValDG() {// 判断树是否为空if (this.root == null) {return null;}return getMinValDG(this.root).val;}/*** 从以node为根的二分搜索树中查找最小值** @param node 树的根节点*/private Node getMinValDG(Node node) {//递归终止的条件if (node.left == null) {return node;}// 递归操作return getMinValDG(node.left);}// 从二分搜索树中找最 大值(在整棵树的最右边)public T getMaxVal() {// 判断树是否为空if (this.root == null) {return null;}Node curNode = this.root;while (curNode.right != null) {curNode = curNode.right;}return curNode.val;}public T getMaxValDG() {// 判断树是否为空if (this.root == null) {return null;}return getMaxValDG(this.root).val;}private Node getMaxValDG(Node node) {//递归终止的条件if (node.right == null) {return node;}// 递归操作return getMinValDG(node.right);}// 从以this.root为根的二分搜索树中删除最小的结点public void removeMinNode() {if (this.root == null) {return;}this.root = removeMinNode(this.root);}/*** 从以node为根的二分搜索树中删除最小的节点** @param node 树的根节点* @return 删除之后的树的根节点*/private Node removeMinNode(Node node) {// 递归终止的条件if (node.left == null) {this.size--;return node.right;}// 递归操作node.left = removeMinNode(node.left);return node;}// 删除操作public void remove(T val) {if (!contains(val)) {return;}this.root = remove(this.root, val);}/*** 从以node为根的二分搜索树中删除元素val的节点** @param node 树的根节点* @param val 删除的值* @return*/private Node remove(Node node, T val) {// 递归终止的条件if (node == null) {return null;}if (node.val.compareTo(val) == 0) {// 更新sizethis.size--;if (node.right == null) {//1、右子树为空return node.left;} else if (node.left == null) {//2、左子树为空return node.right;} else {// 3、左右子树都不为空// 3-1 找到删除节点的后继Node suffixNode = getMinValDG(node.right);// 3-2 更新suffixNode的左右子树
// suffixNode.right = removeMinNode(node.right);suffixNode.right = remove(node.right, getMinValDG(node.right).val);suffixNode.left = node.left;this.size++;// 3-3 返回suffixNodereturn suffixNode;}}// 递归操作if (node.val.compareTo(val) > 0) {node.left = remove(node.left, val);} else {node.right = remove(node.right, val);}return node;}}